Axis of Symmetry

The vertical line that splits the parabola down the middle.

In order to find the Axis of Symmetry in a standard form equation, you must follow the formula of -b
ax²+bx+c 2(a)

For Example

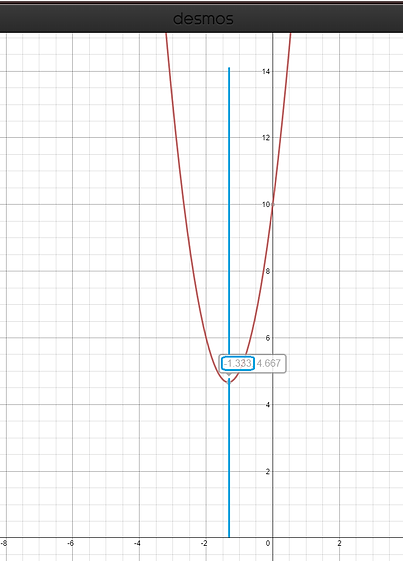
To find the axis of symmetry of the standard y=3x²+8x+10, you must:

Step 1: Make the B value negative (y=3x²+8x+10)

8 turns into -8

Step 2: Divide the negative b value and divide by 2(a) (y=3x²+8x+10)

-8

2(3)

Step 3: Solve

-8 -8

2(3) 6

Therefore, the axis of symmetry is x= -1.33

Question

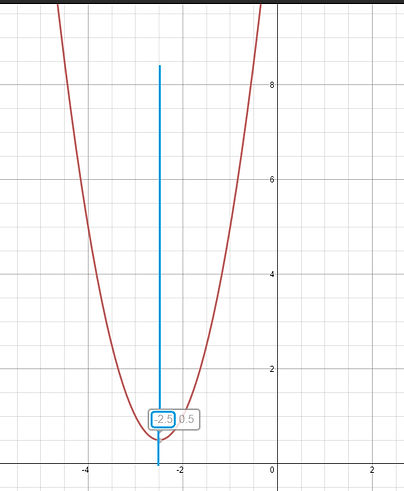
Find the axis of symmetry of the following standard form equation y=2x²+10x+13?

Solution

Step 1: Make the B value negative (y=2x²+10x+13)

10 turns into -10

Step 2: Divide the negative b value and divide by 2(a) (y=2x²+10x+13)

-10

2(2)

Step 3: Solve

-10 -10

2(2) 4

Therefore, the axis of symmetry is x= -2.5