Transformations

Vertical Translation

Horizontal Translation

Vertical Stretch

Reflection

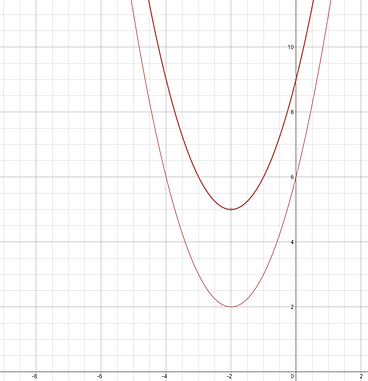
The "k" in y = a (x+h)²+k or the highest or lowest value the graph reaches directly relates to the vertical translation. When two graphs are created, look at the "k" value to see how many units higher or lower a graph is than the other.

Use graph to the left

If the equation for the parabolas are:

y = (x + 2)²+5 and y= (x + 2)²+2 What is the vertical translation?

Solution

y = (x + 2)²+5 and y= (x + 2)²+2

5-2=3

Therefore, a vertical translation of 3 units down occurs to the parabolas

The "h" in y = a (x+h)²+k directly relates to the Horizontal translation. When two graphs are created, look at the "h" value to see how many units further or closer a graph is than the other.

Use graph to the left

If the equation for the parabolas are:

y = (x + 2)²+2 and y= (x+5)²+2 What is the Horizontal translation?

Solution

y = (x + 2)²+2 and y= (x+5)²+2

2-5=-3

Therefore, the horizontal translation of 3 units to the left occurs between the two parabolas

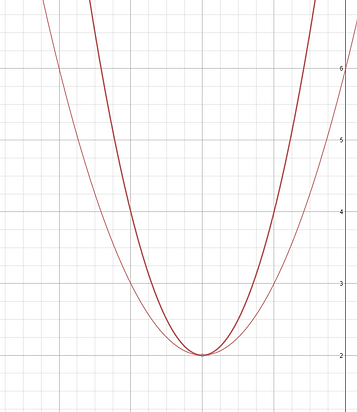
The "a" in y = a (x+h)²+k directly relates to the Vertical Stretch . When two graphs are created, look at the "a" value to see how the step pattern changes to stretch or compress the parabola.

Use the graph to the left

If the equation for the parabolas are:

y = 2(x+2)²+2 and y = (x+2)²+2 What would the step pattern look like?

Solution

y = 2(x+2)²+2 y = (x+2)²+2

X Y X Y 1 1

1 2 2 4

2 8 3 9

3 18 4 16

4 32

5 50

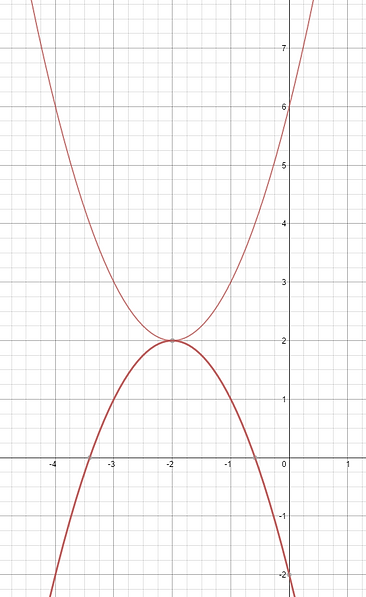
Whether the equation of the parabola is negative or positive can tell if the parabola has a reflection or not. By having the same equation but making the second one negative makes one open up and one open down.

If the equations for a pair of parabolas is

y = (x+2)²+2 and y = (x+2)²+2 How would you make one reflect the other?

Solution

y = (x+2)²+2 and y = -(x+2)²+2